와이블 분포(Weibull Distribution)
와이블 분포(Weibull Distribution)는 1951 년에 스웨덴 수학자 Waloddi Weibull의 이름을 따서 명명된 확률분포이다.
Weibull 분포의 확률 밀도 함수는 다음과 같다.
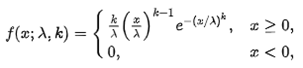
여기서 k는 형상 모수(단 k > 0)이고 λ는 분포의 척도 모수(λ > 0)이다.
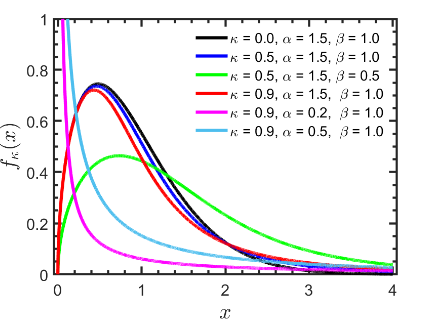
Weibull 분포의 밀도 함수의 형태는 k 값에 따라 크게 변한다. 0 < k < 1의 경우 x가 위에서 1에 가까워짐에 따라 밀도 함수가 무한대인 경향이 있다. k = 1인 경우 밀도 함수는 x가 1에 가까워짐에 따라 0/λ가 되는 경향이 있다. k > 0의 경우 밀도 함수는 x가 1에 가까워지면 0이 되는 경향이 있다.
x가 "고장 시간"인 경우 Weibull 분포는 고장률이 시간의 거듭제곱에 비례하는 분포이다. 형상모수 k는 그 거듭제곱에 4를 더한 값이므로, 이 파라미터는 다음과 같이 직접 해석될 수 있다.
k < 1 : 시간이 지남에 따라 실패율이 감소한다는 것을 나타낸다. 심각한 "유아 사망률"이 있거나 결함 품목이 조기에 실패하는 등 시간이 지남에 따라 실폐율이 감소하는 경우에 발생한다.
k = 1 : 고장률이 시간에 따라 일정하다는 것을 나타낸다. 무작위 외부 사건이 사망률 또는 실패를 유발하는 것을 의미한다.
k > 1 고장률이 시간에 따라 증가함을 의미한다. "노화"프로세스가 있거나 시간이 지남에 따라 실패 할 가능성이 더 높은 부품이있는 경우에 발생한다.
재료 과학 분야에서 강도 분포의 형상 매개 변수 k는 Weibull 계수로 알려져 있다.
이외에 Weibull 분포는 생존분석, 신뢰성 분석, 전기공학에서 전기시스템에 발생하는 과전압, 산업공학에서 제조 및 배송시간, 통신시스템 엔지니어링, 일기예보 및 풍력산업에서 풍속분포 설명 등에 사용된다.